Black-Scholes: o conhecido modelo de precificação de opções

O mercado de derivativos permite ao investidor diversas estratégias de especulação e, principalmente, hedge. E um dos seus conceitos fundamentais é o modelo de Black-Scholes.
Também conhecido como Black-Scholes-Merton, Black-Scholes foi o primeiro modelo amplamente difundido para precificação de opções. É utilizado para calcular o valor teórico das opções usando uma série de variáveis, como os preços atuais das ações, preço de exercício da opção, dividendos esperados, taxas de juros projetadas, tempo de expiração e volatilidade esperada.
A fórmula de Black-Scholes foi desenvolvida na década de 70 por Fisher Black, Robert Merton e Myron Scholes.
No entanto, não é todo preço de opção que pode ser calculado através da fórmula. A opção precisa ser do tipo Europeia. Ou seja, o detentor da opção só pode exercer seu direito do contrato na data de exercício.
Já na modalidade de opções americana, do qual o detentor da opção pode exercer o seu direito a qualquer momento, a fórmula não funciona tão bem.
Caso você ainda não conheça bem este mercado, leia primeiro este artigo sobre o mercado de opções para depois entender como ocorre a precificação de opções no Black-Scholes.
Mesmo calculando o preço de opções europeias o modelo possui algumas premissas. São elas:
- O comportamento do preço da ação corresponde a um modelo lognormal com desvio padrão e média constante
- Não há custos de transação
- Os contratos são divisíveis
- Não há arbitragem possível
- A negociação de títulos e ações é contínua
- Todos os investidores possuem a mesma taxa livre de risco
- A taxa de juros livre de risco no curto prazo é constante
A fórmula Black-Scholes
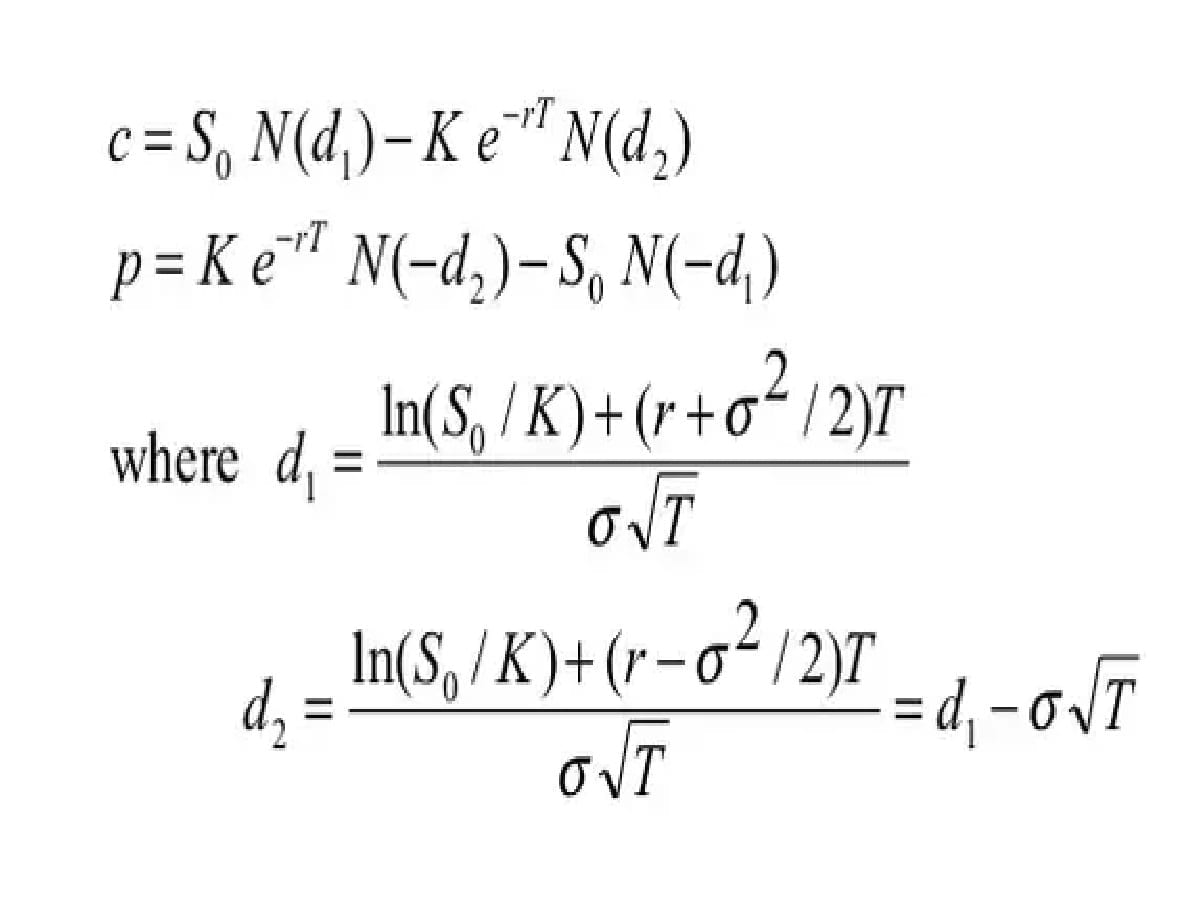
Há uma equação para calcular o preço de uma opção de compra (Call) e outra para calcular o preço de uma opção de venda (Put).
As equações envolvem uma matemática bastante avançada, mas não é necessário nenhum conhecimento matemático para utilizar o modelo.
Existem diversas calculadoras virtuais que poderão calcular o resultado e são utilizadas pelos investidores no mundo inteiro.
No entanto, será demonstrado aqui o que constitui cada equação para uma compreensão do que significa esses cálculos.
A equação para a Call é dada por:
? = ??? ?1 ? −?? − ?? −???(?2)
E para a Put é dada por:
? = −??? −?1 ? −?? + ?? −???(−?2)
Em que:
So = preço do ativo
T = tempo até a data de exercício da opção
r = taxa de juros livre de risco (Selic, no caso brasileiro)
q = taxa ao ano paga de dividendos pela ação. Ou seja, a razão entre o valor anual pago em dividendos e o seu preço.
No entanto, ao usar uma calculadora você só precisará colocar:
- A data de início e vencimento da opção
- Se é uma Call ou Put
- A volatilidade do ativo
- A Taxa livre de risco ao ano (SELIC)
- A taxa de dividendos da ação
- O preço do ativo
- O preço do exercício
Assim, a calculadora te dará o preço da opção no valor presente.
Por fim, o modelo de Black-Scholes é o mais utilizado no mundo para precificar opções europeias de ações por conseguir chegar o mais perto possível do preço real futuro.




