Juros compostos: o que é e como calcular os juros sobre juros?

A maior arma que todo investidor de longo prazo possui ao seu favor é o poder dos juros compostos. Isso porque, com o decorrer do tempo, o efeito dos juros sobre juros no capital investido faz com que o montante aplicado cresça cada vez mais rápido, de forma exponencial.
Da mesma maneira, no caso de dívidas, os juros compostos também fazem com que a dívida total cresça muito rapidamente. Por isso, é fundamental entender, de fato, como funcionam e o quão poderoso é esse tipo de juros, para fazer com que ele esteja sempre trabalhando a favor – e não contra – o investidor.
O que são juros compostos?
Os juros compostos são uma modalidade de rendimento em que os juros são apropriados sobre o montante acumulado, e não apenas sobre o principal. Por conta disso, eles também são conhecidos e chamados, simplesmente, de juros sobre juros.
Para que seus resultados sejam potencializados, as duas variáveis que os investidores devem estar atentos são: a rentabilidade e o tempo. Quanto maior a rentabilidade e o prazo, maiores serão os retornos dos juros compostos – os quais são, inclusive, exponenciais.
E apesar de ser um conceito matemático fundamental, os juros compostos ainda não são bem compreendidos pelas pessoas em geral. Contudo, aqueles que entendem o seu funcionamento podem utilizar dos juros compostos para impulsionar a acumulação de recursos ao longo do tempo.
Além disso, a compreensão sobre esse tipo de juros também é capaz de evitar que as pessoas considerem pegar um empréstimo. Afinal de contas, no caso de uma dívida, os juros compostos são capazes de aumentar exponencialmente o montante devido.
Portanto, como pode ser observado, os juros compostos possuem uma dinâmica que pode trabalhar a favor ou contra o indivíduo. Por isso, é preciso compreender muito bem como ele funciona para garantir que essa arma trabalhe de forma a potenciar a acumulação de capital.
Por que aprender sobre os juros compostos?
Inicialmente, vale ressaltar que o entendimento dos juros compostos talvez seja um dos pontos mais importantes para aqueles que desejam se organizar financeiramente e atingir, em algum momento da vida, a tão sonhada liberdade e independência financeira.
Isso porque os efeitos dos juros compostos são um dos pontos mais importantes no processo de acumulação de capital ao longo do tempo, já que eles potencializam a multiplicação dos recursos investidos. Apesar disso, a maior parte das pessoas, de fato, não conhecem o poder dos juros compostos ao longo do tempo.
Caso conhecessem, desde cedo, esses poderes, sem dúvida a maior parte da população se esforçaria para se colocar na posição de quem recebe – e não de quem paga – juros compostos. Assim, a população poderia ter mais segurança financeira e menos preocupações com dinheiro.
Diferença entre juros simples e juros compostos

O primeiro ponto que deve ser entendido por todos é a diferença entre juros simples e juros compostos. Isso porque, ao verificar a diferença entre esses dois tipos de rendimento, o indivíduo consegue entender, de fato, o poder das aplicações que possuem juros sobre juros.
Abaixo, um resumo e demonstração para cada um desses dois tipos de rendimento:
1. Juros simples
Primeiramente, é preciso entender que, nos juros simples, os rendimentos da aplicação ou a apropriação de juros sobre uma dívida são feitos apenas sobre o valor principal. Em outras palavras, independente do prazo, o percentual de juros é apropriado sempre sobre o mesmo valor.
E por ser calculado sobre com base no mesmo montante, o juro de uma aplicação ou de uma dívida de juros simples é sempre o mesmo. Abaixo, um exemplo de juros simples para demonstrar essa característica de rendimento, considerando uma aplicação de 10 mil reais e com juro de 1% ao mês.
- 1º mês: 1% sobre R$10.000,00 = R$100,00;
- 2º mês: 1% sobre R$10.000,00 = R$100,00;
- 10º mês: 1% sobre R$10.000,00 = R$100,00;
- 240º mês: 1% sobre R$10.000,00 = R$100,00.
Como pode ser observado, o juro de uma aplicação com juros simples é sempre mesmo. Afinal de contas, o percentual de rendimento é calculado com base no mesmo valor, o valor inicial, que no exemplo era de 10 mil reais.
Esse tipo de rendimento é diferente dos juros compostos. Isso porque, como foi colocado, neste tipo de aplicação o retorno é calculado com base no montante imediatamente anterior, o qual considera a apropriação de juros dos períodos precedentes.
2. Juros compostos
Como foi colocado, nos juros compostos, o rendimento de uma aplicação é calculado considerando o montante acumulado. Isto é, considerando os juros apropriados de períodos anteriores.
Por isso, é comum dizer que os juros compostos funcionam como juros sobre juros. Afinal, o retorno calculado de um novo período de remuneração considera também os juros de períodos antecedentes.
Abaixo, o mesmo exemplo utilizado para o tópico anterior, de aplicação inicial de 10 mil reais, com 1% de rendimento, mas considerando juros compostos:
- 1º mês: 1% sobre R$10.000,00 = 100,00;
- 2º mês: 1% sobre R$10.100,00 = 101,00;
- 10º mês: 1% sobre R$10.936,85 = 109,37;
- 240º mês: 1% sobre R$107.847,47 = 1.078,47.
Inicialmente, alguns podem até achar que o cálculo foi feito incorretamente. Afinal de contas, o juro do 240º mês foi mais de 10 vezes maior do que aquele exemplificado do tópico de juros simples.
Contudo, o destaca-se que a conta está, sim, correta e que ela demonstra um pouco sobre a “magia dos juros compostos”. Isso porque, como pode ser observado, a cada novo período, o cálculo do juro é realizado com base no montante imediatamente anterior.
Com isso, quanto mais tempo se passa, maior também é o juro que vai sendo apropriado. Isto ao contrário dos juros simples, em que o rendimento é calculado sempre considerando o mesmo montante.
Como calcular juros compostos?

Depois de compreender as diferenças entre os juros compostos e os juros simples, a próxima passo é saber, de fato, como calcular os juros compostos. Afinal de contas, o seu cálculo não é tão simples quanto o dos juros simples.
Em primeiro lugar, é preciso ter sempre em mente que os juros compostos nada mais são do que juros sobre juros. Ou seja, juros calculados com base no montante anterior (o qual já contém juros de períodos anteriores).
Assim, a fórmula dos juros compostos fica:
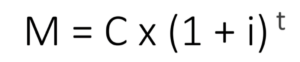
Onde:
- M = o montante acumulado;
- C = o capital inicialmente aplicado;
- i = a taxa de juros;
- t = quantidade de períodos.
Entendendo a fórmula dos juros compostos
É sabido que muitos acreditam que o cálculo dos juros compostos seja complexo. Contudo, isso não é uma verdade, como poderá ser constatado após o entendimento das variáveis da sua fórmula.
Primeiramente, é preciso destacar que o capital inicialmente aplicado (representado pela letra C) não influencia na potencialização dos juros compostos. Isso porque, independente de ser pequeno ou grande, esse capital inicial será sempre multiplicado por uma parte da equação que depende apenas da taxa de juros (i) e da quantidade de períodos (t).
E é justamente o resultado dessa última parte da equação que irá determinar por quantas vezes o capital inicial será multiplicado. Então, independente da quantia, esse capital será sempre multiplicado pelo mesmo número de vezes, caso as variáveis taxa de juros e quantidade de períodos se mantenham.
Assim, o montante acumulado (representado pela letra M) será, simplesmente, o resultado da multiplicação do capital inicialmente aplicado por essa última parte da equação. Isto é, do capital inicial multiplicado por (1 + i) elevado a t.
Por fim, essa última parte da fórmula dos juros compostos é justamente aquela que faz com que haja o fenômeno de juros sobre juros. Isso porque o juro de um período é sempre calculado com base no período anterior, por conta da potência da equação. Veja:
- Taxa de juros (i) = 1% a.m;
- Número de meses (t) = 3;
- Fórmula simples: M = C x (1 + 0,01)³;
- Fórmula completa: M = C x (1 + 0,01)x(1+0,01)x(1+0,01).
Neste caso, o montante final acumulado na aplicação dependerá da multiplicação do capital inicial pelo resultado de uma potência que leva em consideração 3 meses de rendimento a 1% ao mês. A potência do número de períodos (t), portanto, é a parte da equação responsável pelos juros sobre juros.
Exemplo de juros compostos
Os exemplos de juros compostos ajudam a compreender a capacidade desse tipo de remuneração de recompensar aqueles que possuem disciplina e paciência. Sendo que esses são os melhores atributos que um investidor possa ter para aproveitar da magia dos juros sobre juros.
Afinal, é preciso ter disciplina para realizar aportes todos os meses e, ao mesmo tempo, paciência para esperar o tempo passar. Aqueles que consigam manter esses dois atributos, sem dúvida, irão usufruir dos poderes dos juros compostos ao longo do tempo.
Abaixo, por exemplo, um exemplo de um indivíduo que realizou uma aplicação de apenas 200 reais por mês por 40 anos, obtendo neste investimento um rendimento de 0,8% ao mês:
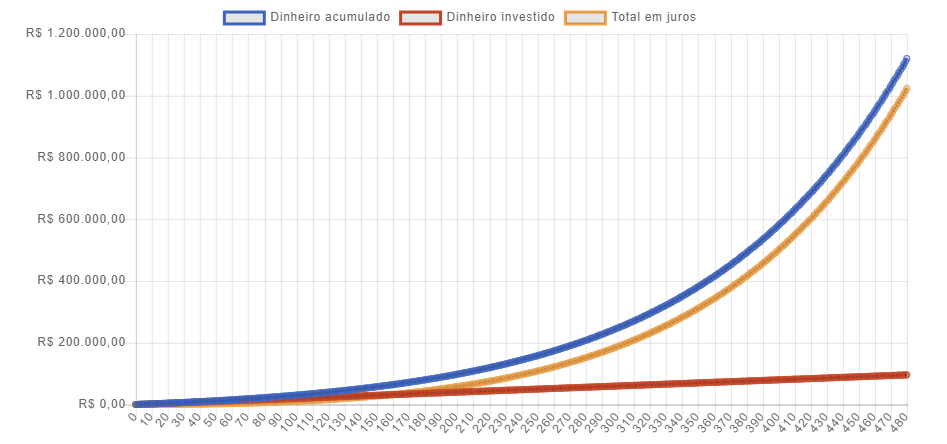
Neste exemplo, os resultados ficaram da seguinte forma:
- Montante aplicado: R$200,00 x 480 meses = 96.000,00 reais;
- Juros apropriados em todo período = 1.024.464,15 reais;
- Total acumulado ao final do período = 1.120.464,15 reais.
Como pode ser observado, os resultados são impressionantes. Com uma aplicação de apenas 200 reais por mês, o investidor que aplicou neste investimento por 40 anos conseguiu acumular mais de 1 milhão de reais, mesmo tendo investido 96 mil ao longo dos 480 meses.
Contudo, para isso, foi preciso disciplina, para aplicar todos os meses, e paciência, para esperar tantos anos para acumular o montante total. E apesar de parecer muito tempo, a realidade é que muitas pessoas irão contribuir para o INSS por mais tempo que isso.
De qualquer maneira, é perfeitamente possível, para reduzir o prazo de investimento, obter uma rentabilidade maior que 0,8% ao mês, bem como realizar aportes mensais com valores superiores a 200 reais.
Como investir com base nos juros compostos?
Após compreender como a fórmula dos juros compostos e de entender como ele pode potencializar os ganhos no longo prazo, muitos indivíduos devem ser perguntar: mas como investir com base nos juros compostos?
Afinal de contas, quem não gostaria de usufruir da magia dos juros compostos para acumular recursos de maneira exponencial? E para comprovar como os investimentos podem garantir essa acumulação, vale citar a evolução do patrimônio de um dos investidores que possui o mais longo histórico de investimento, o bilionário Warren Buffett.
Abaixo, é possível conferir o crescimento exponencial do patrimônio do megainvestidor norte-americano ao longo do tempo, conforme seus investimentos foram sendo atualizados pelos juros compostos:
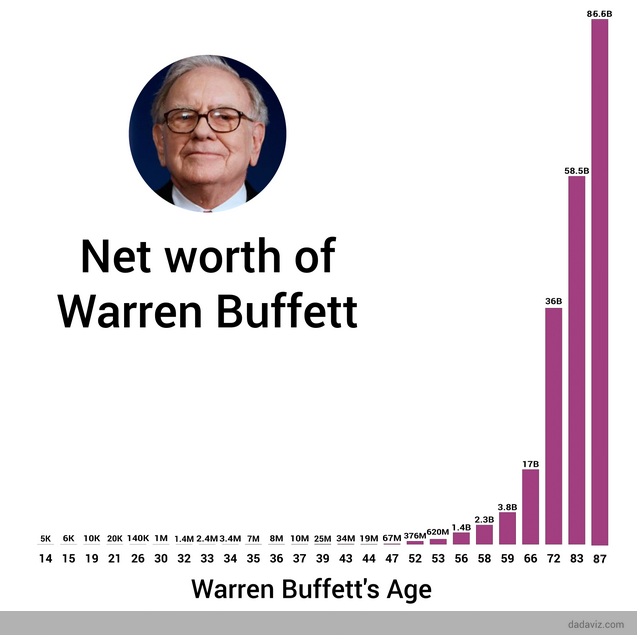
Como pode ser observado, Buffett possuía cerca de 5 mil dólares aos seus 14 anos. Ao longo do tempo, o investidor deu um exemplo de disciplina e paciência, deixando seu capital multiplicar ao longo de mais de 70 anos na bolsa.
Com isso, o fator tempo, da fórmula dos juros compostos, auxiliou muito na valorização do seu patrimônio ao longo do tempo, o qual chegou a ultrapassar a marca dos 80 bilhões de dólares. E não só o fator tempo contribuiu para isso, mas também a variável juros.
Isso porque Buffett é reconhecido por ser um dos investidores que obteve a maior rentabilidade histórica até os dias de hoje. Sendo que o multibilionário manteve o incrível retorno cerca de 20% ao ano de 1965 até 2019 à frente da Berkshire Hathaway.
Para se ter uma ideia, esse retorno acima de 20% ao ano, ao longo dos 54 anos na Berkshire, representa um ganho de 2,744,062%. Mais impressionante que isso, 1 dólar investido com Buffett em 1950 teria se tornado 142.476 dólares em 1193.
Apesar de ser impressionante, esse é apenas um exemplo de atuação dos juros compostos e que, provavelmente, não se repetirá. Contudo, existem outras opções de investimentos com juros compostos disponíveis no mercado.
1. Ações
A primeira forma de investir em juros compostos é por meio das participações acionárias em empresas na Bolsa de Valores. Isso porque, ao investir em ações, o investidor passa a ter direito aos fluxos de caixa gerados pelas empresas, que seriam os juros.
Quando reaplicados, esses fluxos de caixa passam a sofrer os benefícios dos juros compostos. Afinal, o fluxo futuro tende a ser cada vez maior. Ainda, destaca-se que o reinvestimento dessa espécie de juros pode ser realizado tanto pela empresa quanto pelo investidor.
Sendo que:
- Reinvestimento pela empresa: a companhia retém a geração de caixa para reaplicar o capital gerado em suas operações na expansão da companhia. Assim, o fluxo de caixa tende a crescer cada vez mais, por conta dos juros compostos;
- Reinvestimento pelo investidor: o acionista recebe o fluxo de caixa por meio de dividendos da empresa e reaplica esse provento na compra de mais ações da empresa. Então, os ganhos aumentam cada vez mais, conforme o número de ações cresce.
Abaixo, é possível conferir a evolução do investimento nas ações da Taesa (TAEE11). A linha azul representa o rendimento considerando a reaplicação dos dividendos, enquanto a vermelha desconsidera esse reinvestimento:
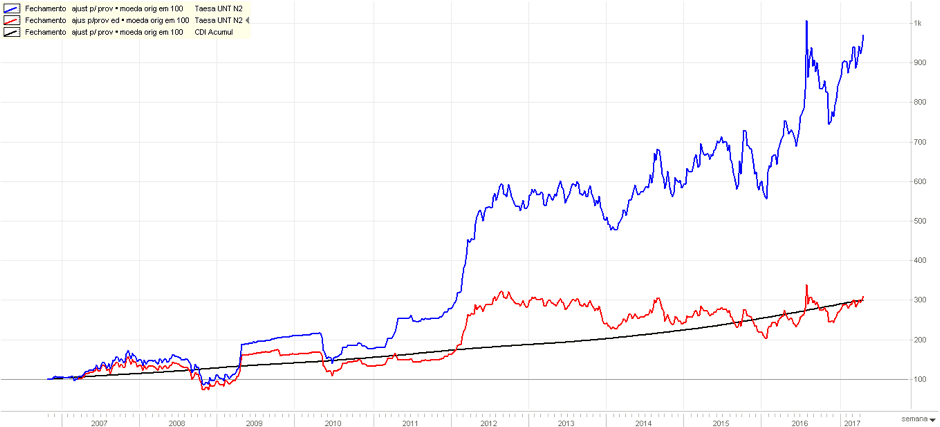
Constata-se que 100 reais investidos em 2007 nas ações units da Taesa teriam se transformado em quase 1000 reais em 2017 caso o investidor tivesse reaplicado seus dividendos. E na hipótese de não ter realizado o reinvestimento, o retorno seria de cerca de 300 reais.
Esse é apenas um único exemplo, mas é preciso saber que, ao verificar o desempenho das ações no longo prazo, a conclusão é de que esse investimento é, sem dúvida, o melhor para garantir a atuação dos juros compostos ao longo do tempo.
Abaixo, o retorno das ações americanas (stocks) desde 1802 em comparação com outros investimentos:
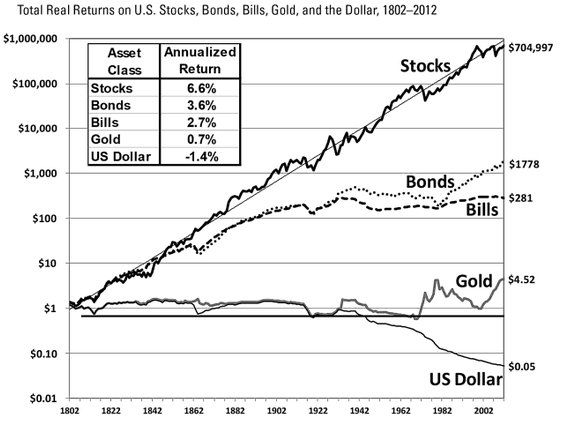
2. ETFs (Exchange Traded Funds)
Para aqueles que desejam usufruir da melhor forma de investir para o longo prazo, de maneira a garantir retornos acima da média com os ganhos propiciados pelos juros compostos, há também a possibilidade de aplicar em ETFs (Exchange Traded Funds).
Basicamente, esse investimento é recomendado para aqueles que reconhecem as vantagens de investir em ações da bolsa, mas que não possuem tempo, habilidade ou o desejo de analisar e de escolher individualmente as ações para investir – o chamado stock picking.
Uma alternativa para isso, então, é investir em ETFs. Isso porque esses ativos funcionam como fundos de investimentos passivos que aplicam diretamente em ações da bolsa, com base em metodologias específicas de investimento.
Isso significa que ao investir em um único ETF o investir está aplicando indiretamente em diversas ações da bolsa. Isto é, nas ações que o fundo passivo investe e que pertencem aos seus investidores.
E para selecionar as ações que irá investir, os Exchange Traded Funds devem sempre seguir uma metodologia pré-estabelecida de investimento. E é por isso que o fundo é chamado de passivo, porque o fundo deve sempre seguir a metodologia de investimento a qual se propôs. Por exemplo:
- BOVA11: ETF que investe nas ações do índice Bovespa;
- DIVO11: ETF que investe nas ações pagadoras de dividendos da bolsa;
- IVVB11: ETF que investe nas ações das empresas do índice americano S&P 500.
Como pode ser observado, cada um desses ETF possui uma metodologia de investimento diferente. Ao investir em um deles, o investidor está diversificando seu investimento de forma prática e barata, sem ter que se preocupar com a seleção individual das ações que irá investir.
3. Fundos Imobiliários (FIIs)
A terceira maneira de investir pensando nos efeitos dos juros compostos é por meio dos fundos de investimentos imobiliários, também conhecidos, simplesmente, por FIIs. E como o próprio nome diz, esses fundos são ativos detentores de imóveis, os quais podem ser, por exemplo:
- Prédios corporativos;
- Shoppings centers;
- Galpões logísticos;
- Imóveis comerciais, em geral.
Isso significa que, ao comprar uma cota de um fundo imobiliário na bolsa, o investidor está, na verdade, adquirindo uma pequena fração dos imóveis que o fundo possui. Sendo que a consequência disso é o recebimento de proventos mensalmente ao longo do tempo, de acordo com o número de cotas, os quais são oriundos dos aluguéis dessas propriedades pelo fundo.
Os proventos, portanto, seriam os juros desse investimento. Então, caso o investidor opte por reinvestir esses juros, ele estaria, de certa forma, acionando a atuação dos juros compostos. Afinal de contas, ao utilizar o provento mensal para comprar mais cotas de FIIs, no período posterior o investidor irá receber, logicamente, mais proventos.
No longo prazo, o reinvestimento desses proventos recebidos fará com que o investidor acumule um número de cotas de FIIs cada vez maior. Assim, o seu patrimônio acumulado em fundos imobiliários crescerá exponencialmente ao longo do tempo, por conta da atuação dos juros compostos.
4. Renda fixa
Por fim, outra modalidade de investimento que possui os benefícios dos juros compostos é a renda fixa. Basicamente, esse tipo de investimento é realizado em títulos de crédito públicos e privados emitidos no mercado. Sendo que:
- Títulos públicos: títulos de dívida do Tesouro Nacional emitidos pelo governo no mercado que prometem um percentual de rendimento pré-estabelecido ao investidor;
- Títulos privados: títulos de dívida emitidas por diferentes empresas que captam recursos no mercado e que prometem uma remuneração ao aplicador por isso.
Vale destacar que, na maioria das vezes, os títulos de renda fixa possuem muito menos risco do que investir em ações de empresas. Afinal de contas, grande parte desses títulos possuem garantias e rendimentos conhecidos pelo investidor na hora da aplicação.
Por outro lado, esses títulos também possuem uma remuneração, também, menor. Afinal de contas, quanto menor o risco, menor o retorno; e, quanto maior o risco, maior o retorno. Por isso, o mais adequado é diversificar os investimentos com aplicações de renda fixa (títulos) e de renda variável (ações e ETFs).
Como evitar o pagamento de juros compostos?

Tão importante quanto utilizar os juros compostos a favor dos investimentos é compreender o seu funcionamento para saber como evitar o pagamento de juros compostos em dívidas e financiamentos.
Isso porque a dinâmica dos juros sobre juros não é exclusiva dos investimentos. Na verdade, o fenômeno dos juros compostos também se aplica à vasta maioria dos passivos onerosos disponíveis no mercado para as pessoas, como:
- Financiamento imobiliário;
- Financiamento de veículos;
- Empréstimo rotativo;
- Empréstimo consignado;
- Cheque especial.
Ao adquirir ou usufruir de recursos por meio de algum desses financiamentos, o indivíduo está se colocando na ponta contrária dos juros compostos. Afinal de contas, ele será o responsável por assumir e pagar o montante acumulado na dívida, o qual é calculado com base nos juros sobre juros.
É por conta disso que muitas pessoas adquirem determinados empréstimos e acabam se surpreendendo com o crescimento exponencial da dívida. Sendo que isso acontece justamente por conta dos efeitos dos juros compostos nesses passivos.
Além disso, destaca-se que na maior parte das vezes a taxa de juros desses empréstimos é muito alta, principalmente para os créditos disponibilizados para a pessoa física. Por conta disso, o poder dos juros compostos é observado na multiplicação do montante devido em pouco tempo.
Portanto, é preciso que todo indivíduo avalie muito bem a necessidade de realizar empréstimos e financiamentos antes de fazê-lo. Assim, alguns podem evitar de se colocar na ponta contrária dos juros compostos, assumindo a infeliz posição daquele quem paga os juros sobre juros.
Pagamento de juros compostos por empresas
Por fim, vale apenas ressaltar que, para algumas empresas, adquirir financiamentos, mesmo pagando juros compostos, pode valer a pena. Isto acontece, via de regra, no caso em que o ROIC (Return On Invested Capital) da companhia – que representa sua rentabilidade – é maior que o custo médio de sua dívida.
Abaixo, é possível verificar o retorno da Localiza (RENT3) em relação ao custo médio de sua dívida:
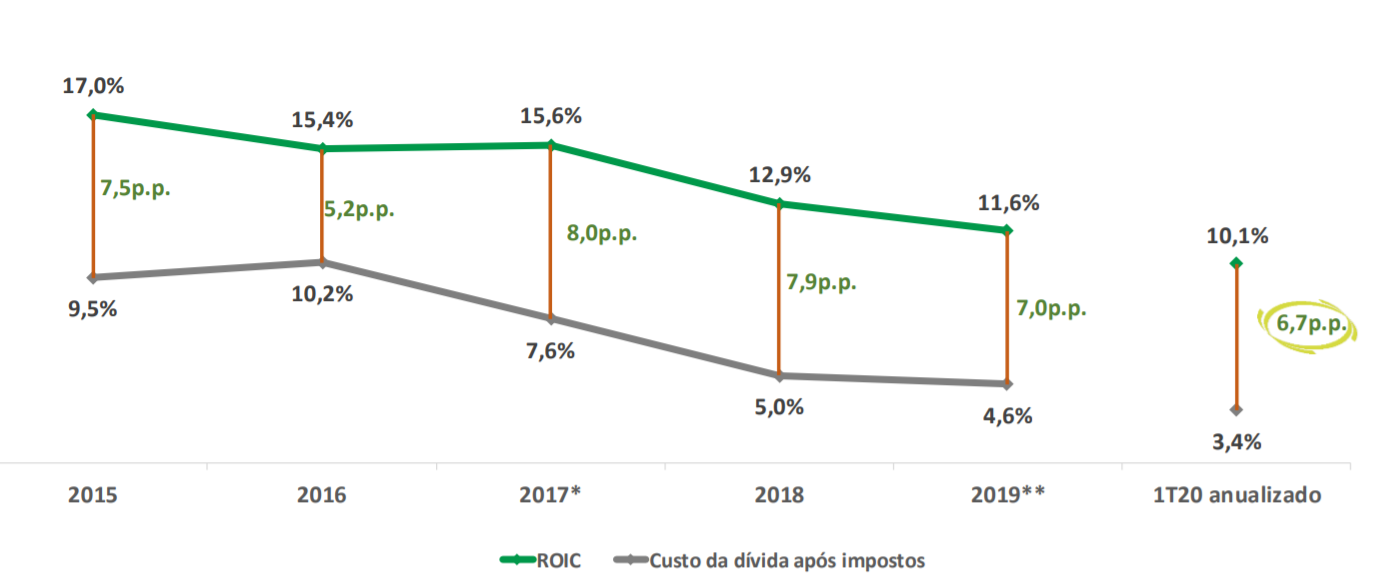
Como pode ser observado, a Localiza, assim como diversas outras empresas de capital aberto na bolsa, está gerando valor para seus acionistas, mesmo pagando juros compostos para terceiros em suas dívidas.
Isso porque, apesar de pagar uma média de 3,4% ao ano de dívida para seus credores, a companhia consegue rentabilizar o capital de terceiros em 10,1% ao ano. Em outras palavras, ela paga 3,4% ao ano em juros compostos, mas obtém 10,1% ao ano em retorno, o que resulta em um spread para a empresa e seus acionistas de 6,7%.
Duas explicações para esse resultado são: a alta rentabilidade financeira da empresa e o baixo custo da dívida. Por conta disso, esse modelo de geração de valor não pode ser replicado pela pessoa física.
Afinal, indivíduos não conseguem rentabilizar recursos como uma empresa, bem como não são capazes de adquirir financiamentos tão baratos quanto companhias. Por isso, o ideal é que a pessoa física se mantenha sempre longe de dívidas e empréstimos, de modo a não ser a ponta que paga os juros compostos.
Qual a fórmula para calcular juros compostos?
A fórmula para calcular os juros compostos é M = C x (1 + i)^t. Onde M é o montante acumulado, C é o capital inicialmente aplicado, i é a taxa de juros e t é o prazo, em períodos, da aplicação.
O que é juros compostos?
Os juros compostos são uma forma de multiplicação de capital em que a apropriação de juros é calculada com base no montante acumulado na aplicação ou na dívida, já considerando juros incidentes de períodos anteriores. Há, portanto, o efeito de juros sobre juros.
Quando se usa juros compostos?
Os juros compostos são usados em aplicações financeiras na acumulação de recursos ao longo do tempo. Além disso, são também utilizados na apropriação de juros sobre empréstimos e financiamentos.
Quando juros simples rende mais que juros compostos?
O juros simples rende mais que os juros compostos quando o período de apropriação de juros é menor que 1. Depois disso, os juros compostos sempre renderão mais que os juros simples.
O que é mais vantajoso: juros simples ou compostos?
O que é mais vantajoso, entre os juros simples e juros compostos, depende da posição em que a parte se encontra. Para aquele que paga, os juros simples são melhores, porque são menores. Já para aqueles que recebem, os juros compostos são mais vantajosos, pois são maiores.
Bibliografia para juros compostos
https://www.al.sp.gov.br/StaticFile/ilp/Mat.FinancConvertido.pdf
http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/1672-8.pdf
http://www.casio.edu.shriro.com.au/products/fx9860gau/pdf/compoundint.pdf
https://www.rcboe.org/cms/lib/GA01903614/Centricity/Domain/11348/ch12L4.pdf















